



The red planet (Mars), an apple, apple seed, plant embryo in apple seed
Research (link1, link2) shows that plants do not grow exponentially, even in the early stages. They grow slower. Their mass increases with the square root of time. Simple, 2 dimensional simulations suggest that it is because plants growing according this pattern win from faster (polynomial of the third order, see link3) and slower (polynomial of the first order, see link4) growing specimens. The second-order plants beating the third-order plants show it to be an advantage to reduce production capacity in favour for more competitive ability during the earlier growth at high densities. However, it does not work for the first-order plants while competing with the second-order plants. They simply cannot occupy the space conquered by a higher competitive ability in the earlier stages. So, the second polynomial for plant growth is Darwin’s winner and arises in the struggle for life.
There is an interesting analogy between a biological and physical polynomial of the second order, if one accepts a hypothetical transformation: The plant is changed from an energy or mass intercepting in an energy or mass attracting phenomenon. It is illustrated in figure 1.
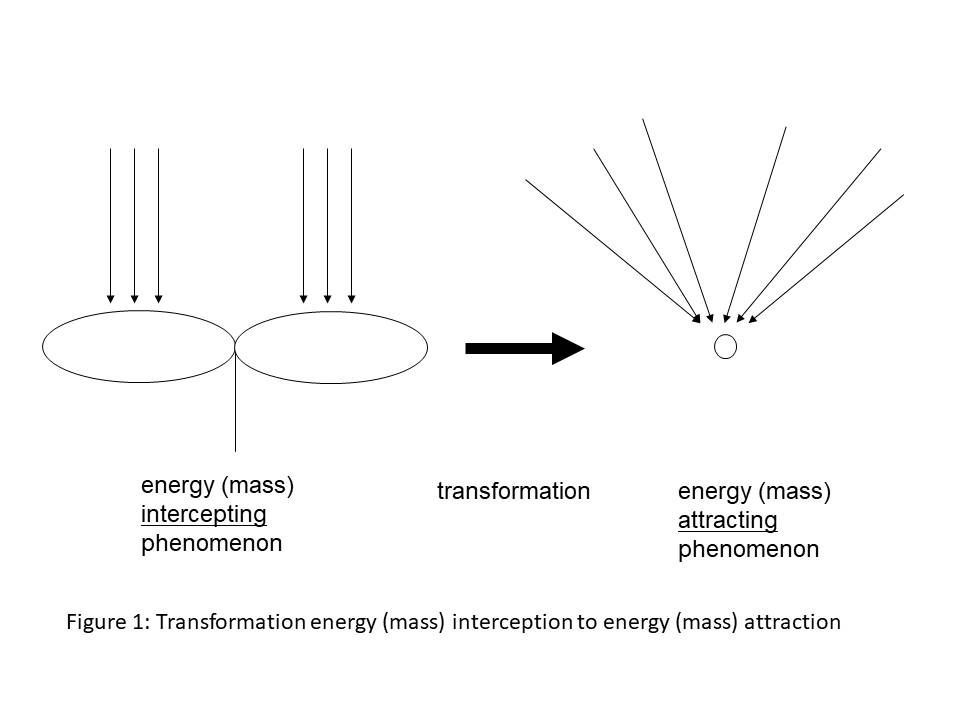
The next question is how the attracting force would look like if the transformed plant mass would still increase with the square of time.
The plant has to create a potential that makes the speed of the incoming energy increase linearly with time, i.e. with a constant acceleration. Doesn’t this look like the law of gravity of Newton?
In addition,, notice the other way round: Einstein states space to be bended by gravity. With a little imagination it as if the space opens to “intercept gravity”.
Is this analogy a coincidence? Someone, who has the slightest doubt, considers the hypothesis that both phenomena have the same cause. He can use this generalization for further theorizing, but only if he tries to find evidence of the contrary, as stated in the guidance in an earlier paper, arguing with the theory of science (link5):
One can use a generalization for theorizing, if there is any indication for it, if one immediately searches for falsifications.
So, we generalize here a life phenomenon and a physical phenomenon and state that they arise, apart from the transformation interception/attraction, in the same way. Of course, in the next papers, we will try to find the falsifications. It is interesting anyway, because also succesful falsifications will clarify more the distinction between life and the other physical world. When is life life?