A possible objection to the idea that the force of evolution will generate the physical forces (see link1, link2) is the observation that the physical Newton world will evolve to an Einstein world at larger scales and the expectation that this will not be the case in Darwin’s world. There will not be relativity in the biological world. But this is a little too fast. There are relativity effects in life. A species with a higher metabolic rate, i.e. energy consumption, tends to
- be bigger and
- live longer
then a species with a lower rate. Kleiber quantifies this with the following formula:
B=M2/3 (2)
where B =metabolic rate and M = mass.
Ad 1. Bigger with a higher metabolic rate
To falsify that the Kleiber phenomenon is the same relativity described in physics we should compare the formula of Kleiber and the relation between velocity and energy according to the theory of relativity:
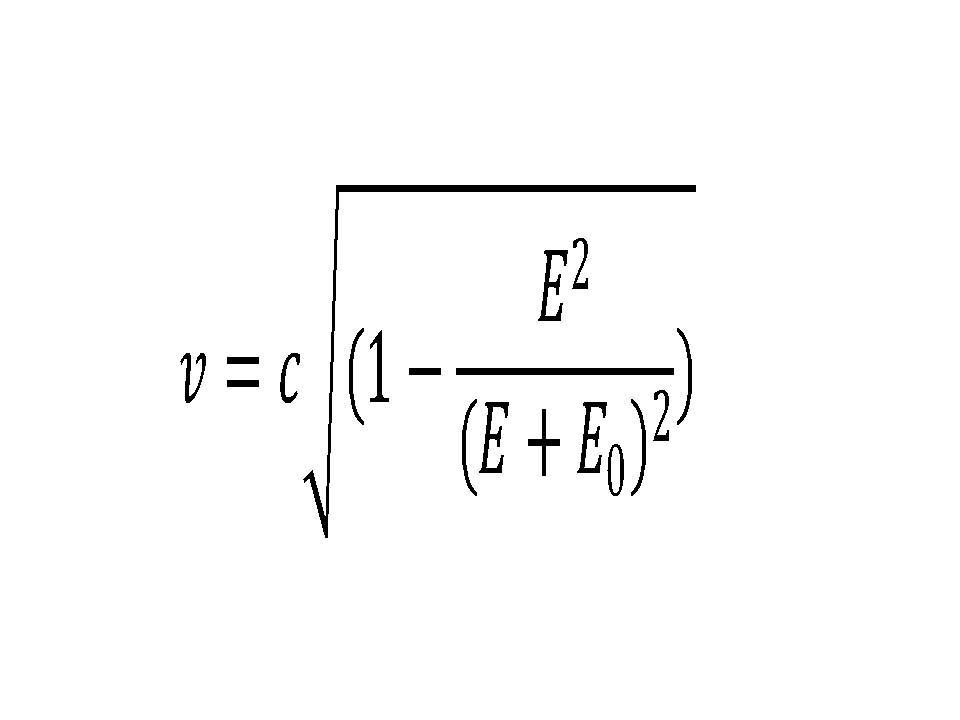 (3)
(3)
With c = velocity of light
E = the energy of a mass at rest
E0 = the additional energy of a moving mass
At first sight they seem very different, but notice that the last formula evolves to the following one, when the additional energy is very small compared to the energy of the mass in rest:
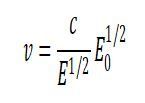 (4)
(4)
Formula 2 and 4 are very similar with v = B and M = E0 and c/E1/2 = constant.
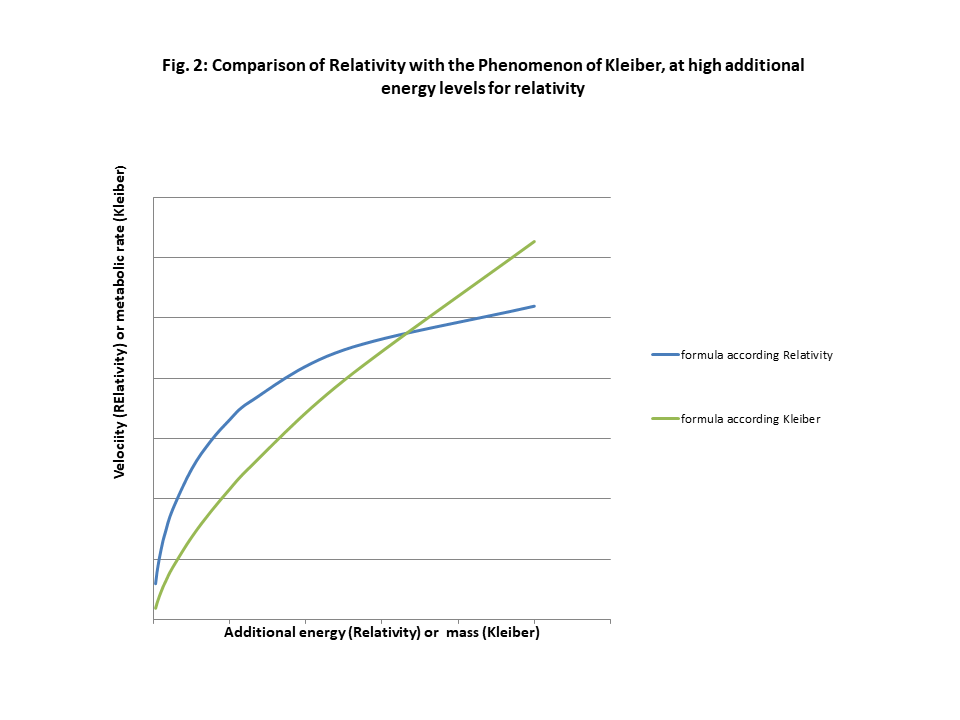
The following figure (1) shows also it to be difficult to prove that observations of the relation between metabolic rate and biomass are better described by the Kleiber formula then the following formula constructed in the same way as the one for relativity.
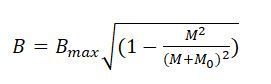 (5)
(5)
With Bmax = maximal metabolic rate
M = the mass with metabolic rate 0
M0 = the additional mass necessary for a metabolic rate > 0
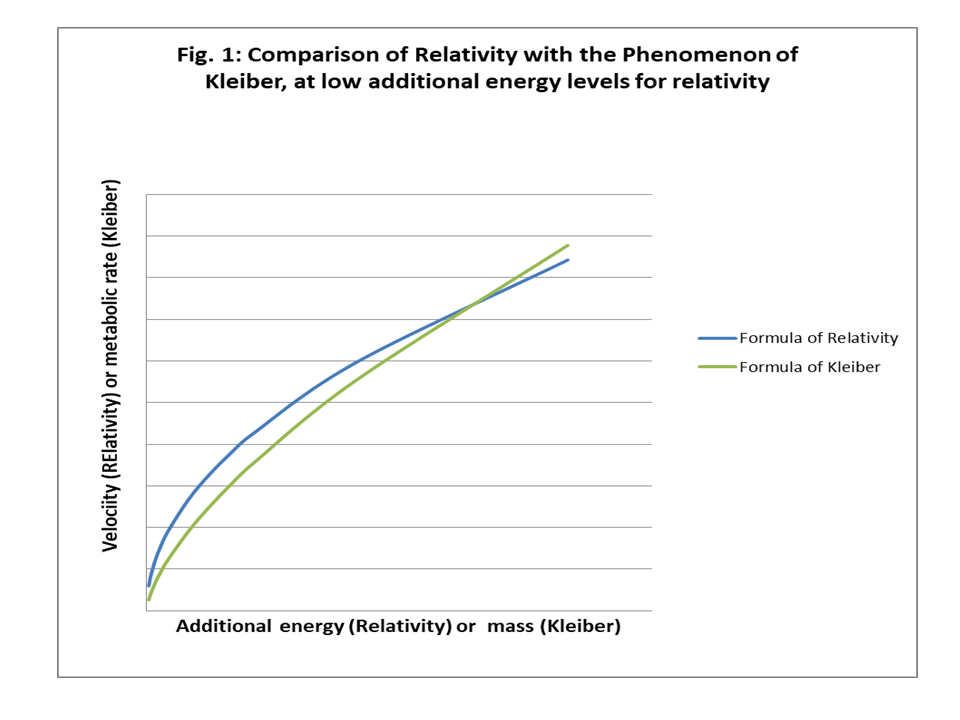
Notice that in figure 1 M0 is very small as compared to M. The difference between formula 2 and 5 is found at large masses M0 as compared to M, see figure 2. The crucial difference is the asymptote for a maximum rate in formula 5, with the Lorentz transformation. The question is if the Kleiber equation is the one showing a weakness here, as it presumes no maximum for the metabolic rate.
Ad 2. Living longer with a higher metabolic rate



Can you say something about time when you see these wild clover pictures? Answer at the end of the page
A bigger organism with a faster metabolic rate lives not only longer, it is also slower in reaching its next development stage, for example maturity. The relative age of two species born at the same moment measured as distance to death or development stages such as maturity is lower for a faster metabolizing species. Children are quoting: One year for a dog is seven years for a human being. The famous twin paradox is even applicable. If it would be possible to divide tissue from a species into two identical parts and transplant one to another faster metabolizing species and put it back after a certain time it will have aged less than the part which stayed behind. This is exactly what the Theory of Relativity predicts, isn’t it? If this tissue cannot “observe” that it is transplanted to another world, it will only sense a temporarily acceleration in speed, i.e. metabolic rate.
The relativity in age, as described here, adds possibly something to the Theory of Relativity. Not being a physicist the author should be careful, but in his interpretation Einstein starts his fundamental reasoning by observations of space. Using the constant speed of light he concludes the relativity in space. The relativity in time is deducted from it. But we can do it here the other way round by starting with observations of time. The big question is how we can become aware of changes in time. Is it really that we observe time itself or do we notice it as a reference to changes in an object? If one can only see changes of a dog (the senses are not good enough to determinate the size) one can only state that one time unit is passed when one sees clearly the signs of new features, e.g. maturity. If a second person with the same constraints could only observe a human being, he will also state that one time unit is passed when he would see the clear signs of maturity. Having another reference system, the children mentioned above can correct them by stating that one year is passed for the dog observer and at least seven years for the human observer. Notice, that the children would have a problem to prove it, when the earth would not rotate and would stand still in space. The suggestion is clear: We can only be aware of a change of time by clear changes in the development stages of a phenomenon. When this phenomena repeats in a constant rhythm (generations of dogs, generations of human beings, waves of light?) we get the idea that we observe absolute time.
The next question is why this relativity occurs. In the biological world an idea can be (this is still a think experiment) the assertions:
- When an organism is able to intercept more energy in the same time interval, and the processing is based on the same chemical metabolism with a maximum speed, it will have to have more mass to process this extra amount of energy.
- But this new mass will be less efficient: The extra energy will have to pass the old mass to reach the new mass and there will be extinction (see e.g. literature about extinction in plant canopies) The organism can reorganize and make the old mass less dense and let more through, but then it will not use the old mass completely. Maybe it will wait a little longer to duplicate its units and that will implicate a slower development. Simulation should show that this gives an advantage in the competition.
Solution question pictures: You can tell nothing about the time elapsed between the first two pictures of the clover leaves. But the third picture tells us that the clover is at least in a latter development phase, the flowering phase.