Introduction

(9-3-2023: this paper was corrected, as the mutation rate for introducing new factors was 5% instead of 20%. As the conclusions stayed the same, and an additional research showed the mutation rate not being important, we considered it right to correct the paper and not make a new one)

New developments in science suggest gravity not to be a fundamental force but emerging in a world governed by changes in entropy (information).

Without really understanding this theorizing, we used this basic idea for a new sixth falsification of  the generalization of gravity and plant growth, showing both a second order polynomial in the direction of time (link1).

First, we had to develop an idea about what information means in the plant growth and especially in the simple model we used to describe (link2) and to simulate plant growth (link3).

Remember this is a think experiment: New ideas are allowed, even if they are provocative. Starting point is the division of the plant in a productive and an unproductive part, as done in an earlier paper (link2). The reasoning towards the new idea evolves as follows: If we suppose that evolution has optimized the productive part (photosynthesis of the plant), we have to conclude that only the unproductive part can contribute to a change in information in a plant. We had concluded in the  paper mentioned before that the unproductive part must be the competitive part of the plant, because according the evolution theory every part in a living organism should have a function, . Combining both conclusions we have to assert the new idea: a change in information means a change in competitive ability. It suggests that the plant cannot only increase its competitive ability by simply increasing its unproductive part, but also by changing the way it is competing, changing the information. E.g. it can not only compete by height , trying to overshadow a higher plant, but also by making e.g. a poisonous substance for another plant. The information would increase by introducing a new factor.

Now we can formulate the sixth falsification. A differentiation in competitive ability, i.e. an increase in information, cannot cause the emersion of a polynomial of the second order as winning from polynomials of higher order. It should falsify the generalization of gravity and plant growth, as the latter will not show a polynom of the second order in the direction of time.

Notice, an earlier falsification, the fifth (link4), succeeded in making disapear the winning second order polynomial in plant growth by bending the leaves: The productive part, the energy interception, is not fundamental for a polynomial of the second order in plant growth.  A striking question comes now forward:  Will plant growth follow the newest ideas of gravity in the sense that not the interception energy is fundamental for its characteristics? Does re-emerge a polynomial of the second order by  differentiation in competitive ability, i.e. the increase in information?

Methods

To verify the sixth falsification we made again a simulation as simple as possible, in the same way as published in an earlier paper (link3).

We compared again a polynomial of the second order and the third order. We already showed that a second order wins form a third order in the earlier ages. It invests earlier in the unproductive part, in the competitive part. At later ages the investment does not pay out anymore as the bigger productive part of the third order starts to produce also a bigger unproductive part, see table 1.

Tabel 1: Productive mass (y_P(t)), non-productive, competitive mass (y_NP(t)) and total mass (y_(t)) as function of time of plants growing according a polynomial of the second order and the third order. The colour dark red and dark purple indicates the winning order polynomial at that moment: The competitive mass is bigger, i.e. the stem is higher. Dark red is for the plants investing initially more in competitive ability and purple for the plants investing initially more in production. The colour green indicates a draw.

So, we could only expect that circumstances which lead to short lives give advantage for second order polynomial plants. It led to experiments where we varied in different parameters related to suppressing higher ages.

We  already have seen in earlier papers that second order polynomial plants  with straight leaves were winning, when

• they had a lower maximum age
• offspring was not randomly distributed in space and time but concentrated around the mother plant.

Each strategy, lower maximum age and concentrated offspring, was winning on its own from the opposite, higher maximum age and random distribution respectively (link5), but only when the leaves were straight horizontal. All this disappeared when the leaves were bended.

The assumption that differentiation  leads to better competition and therefore to earlier deaths for the opponents  implies that we had also to investigate variations in

• mutation rates, as we expect that a faster introduction of new factors would cause a lot of deaths, preventing the plants to reach higher ages
• amount of factors as a measure for the differentiation, for the same reason

We needed also assumptions about:

• the size of the seed. In table 1 you can see that a bigger seed can make the plants germinate in a later phase. For the right understanding: Time in table 1 starts in such a case later, e.g. 2 steps later when the seed has e.g. the size of 4. Of course, the amount of the offspring is the total mass of production divide by the size of the seed. It could be an advantage for the second order polynomial plants, as they could introduce immediately after germination a winning competitive part.
• how much the size of the factor in a plant needs to be bigger then the same factor in another plant to win.
• if the height of the bended leaves are still important in the competition when new factors are introduced.
• how many factors should be introduced in one timestep
• how big the new factors should be in each timestep. Notice, each quantity for the new factors meant a smaller quantity for the old factors.
• how big should the expected empty space to be to conquer.

By trial an error we proceeded until we saw appear a second order polynomial winning from a third order.

RESULTS

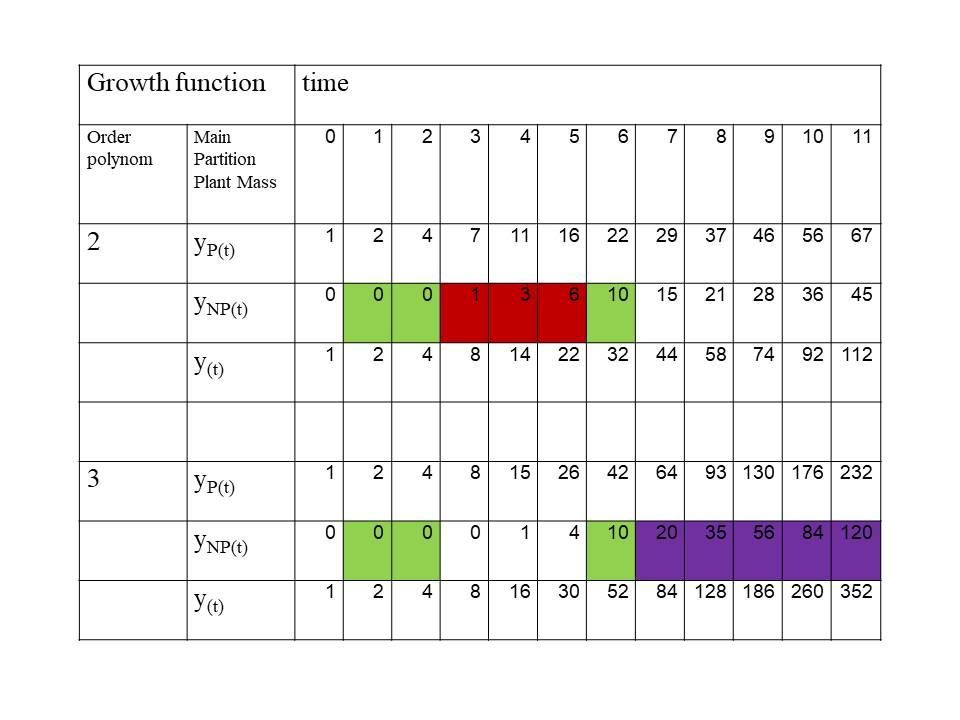
We succeeded in the end to make the second order polynomial winning from the third order (see figure 1)

The following parameters led to this result :

1. 1. the maximum age was 7,
   2. the offspring around the mother plant had for 80% no dormancy instead of the 60% in earlier experiments,
   3. new factors were introduced at a mutation rate of 5%,
   4. the amount of factors was 12,
   5. the size of the seed was set to four,
   6. the size of a factor of a plant was set to be 3 times bigger than the size of the same factor of another plant in order to make the first plant to win,
   7. the competition of the hight of the bended leaves was neglected when other factors were introduced,
   8. The starting plant had one factor not being height, which was as big as the unproductive part was. Each new factor had only the size of one unit, which meant that the size of the first factor was only diminished by one for each new factor. It implied that a new factor would only be winning for a plant, if there was zero for this factor in the adversary. Preliminary research showed it to be disadvantage to diminish fast the size of the factor which was there from the beginning: It would be too fast smaller than one third of the original size, and then the new factor plants will lose too fast from the old plants. Also preliminary research showed that it was more important to invest again in new factors then to make the recently introduced factors bigger.
   9. The maximum size of the space to conquer was 250.

Of course, this is not a proof for a statement that the second order is overall winning. But remember we were entitled to search for a winning second order because we found it in reality, i.e. in plant growth experiments (link6).

Besides, the case of second order polynomial growth is stronger when the parameters 1 up to 10, mentioned above, are winning from variations. The now almost “constructed” winning second order polynomial would emerge by evolution.

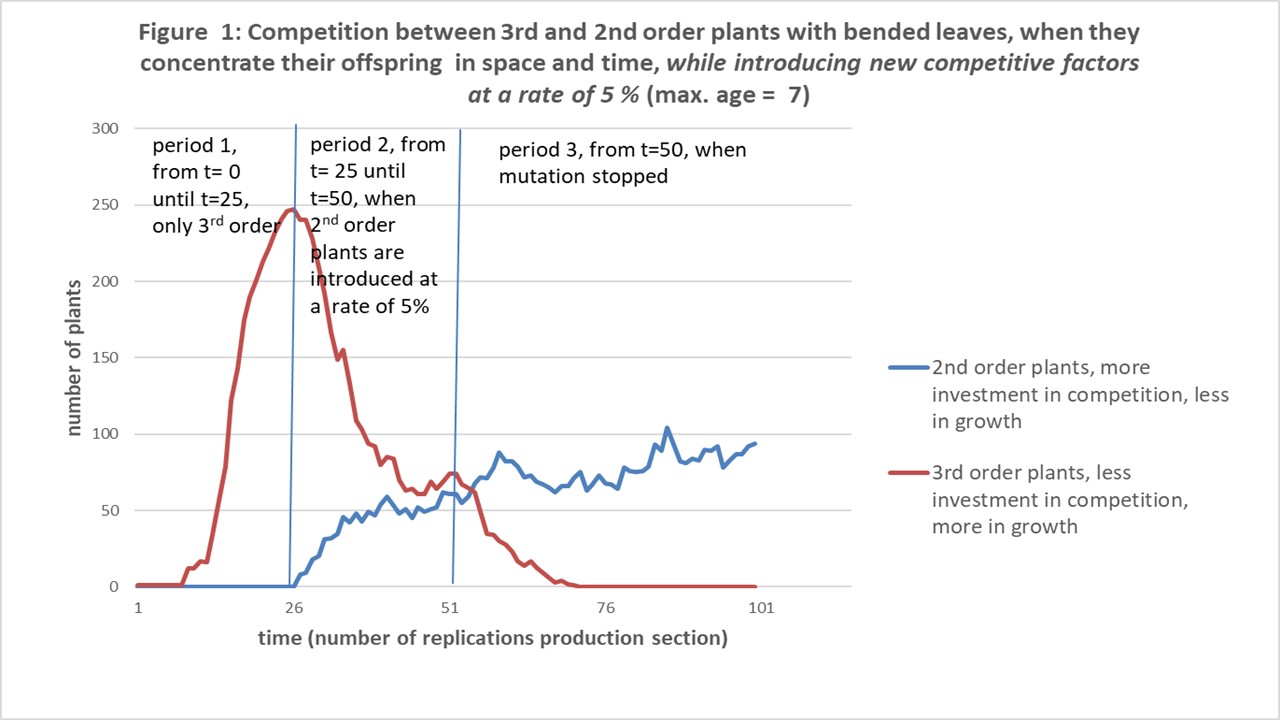
We succeeded in the first two parameters. Starting with parameter 2, we saw that at an age of 9 the plants were winning when concentrated in space. First, it was not the case, but an increase in concentration in time, i.e. more plants germinating without dormancy, made it happen, see figure 2. Notice, concentration of germination in time, is always winning, as the non-dormant seeds are replacing the dormant seeds on the same location.

Parameter 2: Differentiating plants concentrated in space were winning from differentiating plants randomly distributed over space, see figure 2.

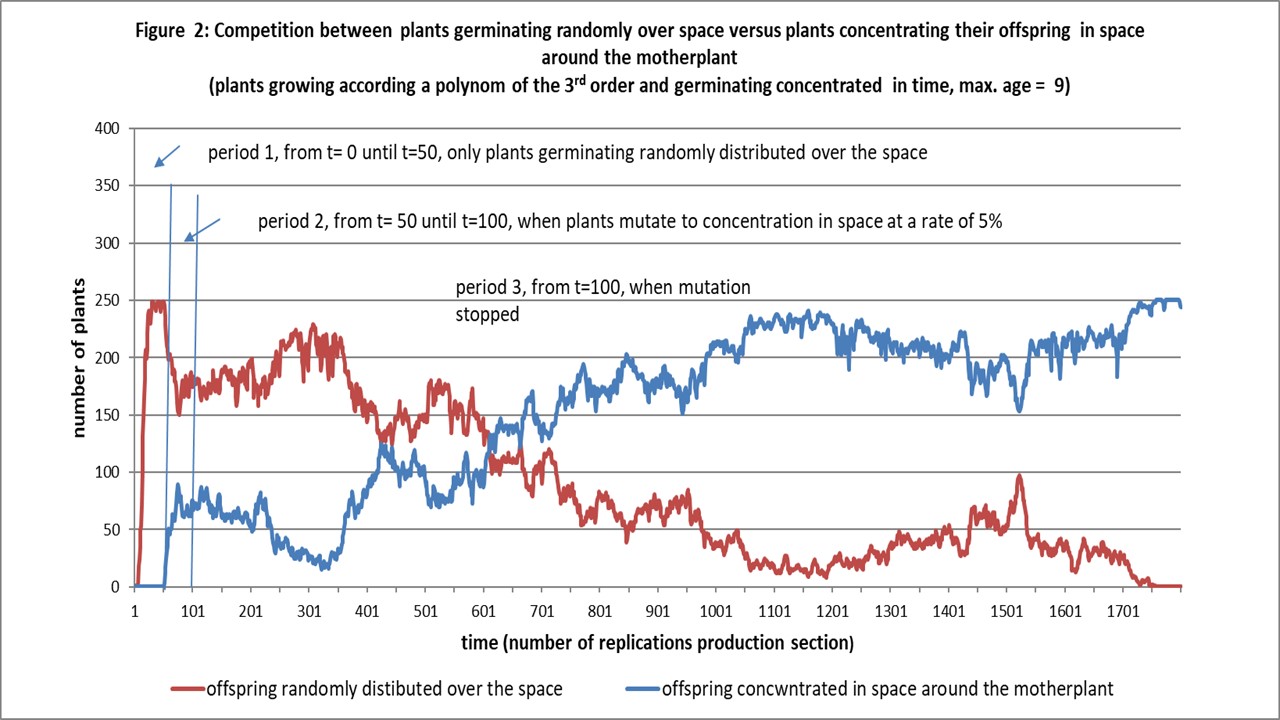
Parameter 1: Plants with maximum age 7 are winning from older plants, aged 9, in all three iterations we tried. They were also winning from younger plants, aged 6, in two out of three cases.

Parameter 3:  Preliminary research shows a change in mutation rate not to be important.

4 and 8: A larger amount of factors and faster introduction of factors will cause higher death rates favoring second order polynomials, but we need further testing. One big question is if there are ideal figures for these parameters and if so, what values do they have?

Parameter 5.  The first results show seeds of size 4 to win from seeds 2.

Parameter 6 is an assumption, based on the observation that defence is easier than attack: The defence can be up to three times smaller than the attacking size to get a draw.

Parameter 7 has a special position: To get secondary polynomial growth it was  necessary up to now to neglect the height as an important competition factor when another factor was involved . To be clear: When another factor was introduced the competition in height between 2 plants was not evaluated. It was supposed to be too weak in respect to the new factor. An argument could be that bended leaves are not really covering other lower leaves especially in respect to light coming in at lower angles than from vertically above.

As mentioned before, the first tests with parameter 8 showed interesting results: Loosing too fast “identity”, e.g. by appointing randomly the size of the competitive, unproductive part to the 12 factors , leads to losing the competition.

We have still to investigate parameter 9. Earlier experiments show that increasing the empty space could alter the results, especially by an increasing maximum age. Complicating is the observation that this is only possible if there is suddenly an appearing of a bigger empty space, immediately raising the question how a plant would know that. They will be prepared for the normal situation: full competition in a crowded space.

A lot more experiments are necessary varying the factors, always watching if the conclusions made for preliminary factors are not changing and if in the end the concluded secondary polynomial growth is still there.

But, the author wanted not to wait with a publication, after the vanishing of the secondary polynomial growth as a result of the fifth falsification: It can reappear  because a sixth falsification did, as a surprise, a contrary job. The justification is the appearance of this phenomenon in reality.

Puzzling is the fact that a “crazy” think experiment seems to help to guid us in understanding fundamental plant growth.