Introduction

Most models describing the relation between plant mass and time assume initial plant growth to be exponential. Especially models consisting of one equation do. Thornley (1990) discusses them. This paper summarizes and evaluates his argumentation and at the end it refers to other related papers showing that the assumption is not correct.
De Chanter-, Gompertz- and logistic growth equation
Thornley (1990) describes the De Chanter equation. It is the most interesting of the discussed one equation models because it contents all the aspects of the other two, the Gompertz and the logistic equation.
dy/dt = RGR y (1 – y/yMAX) e-Dt (1)
Where
RGR = relative growth rate (time-1)
y = plantmass (mass)
t = time (time
yMAX = maximal mass of the plant (mass)
D = decay of RGR ( – )
RGR and D are constant. In this formula 3 factors determine growth:
- The first factor, RGR y, is the basic idea of exponential growth: The growth is linearly related to the plant mass. The share of the growth machinery is supposed to be constant.
- A second term (1 – y/yMAX) explains that the growth depends on the amount of substrate. A maximal amount of substrate means a maximal size of the plant (yMAX). The closer the plant mass approaches this maximum size (y –> yMAX), the less substrate rests and the slower growth is.
- A third term, e-Dt indicates that decay delays growth. This is caused by:
-
- Degeneration and aging
- Development and differentiation
-
We can derive the logistic and the Gompertz- equation by removing the third and the second term respectively. Thornley (1990) didn’t accept the Richard’s equation.
All these models implicate that a young plant grows exponentially, as
- The term ad 2 can be neglected, if there is enough substrate available (as y << yMAX).
- The term mentioned ad 3 can also be skipped (D=0), if we consider that degeneration and aging (ad 3a) are of no importance in the beginning of plant life and that there is no known reason that the share of the growth machinery is changed by initial development and differentiation.
As stated before, the equation becomes without these terms exponential:
dy/dt = RGR y (2)
Where y,t = see equation 1
Notice, that the integral of this equation shows a linear relation between logarithm of plant mass and time.
ln y = ln y0 + RGR t (3)
Where
y,t = see equation 1
y0 = plant mass on time = 0 (mass)
By representing all the models in a logarithm form we can illustrate again that they implicate exponential growth in the beginning, as is shown by the initial linearity in all lines in figure 1.
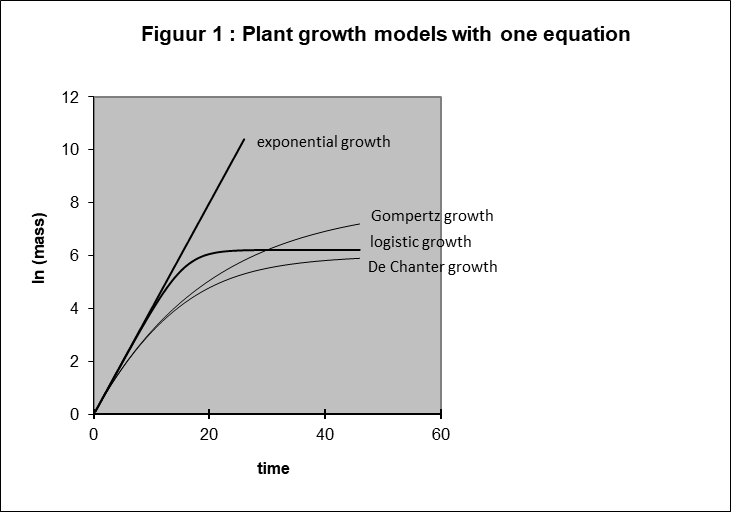
Evaluation
Thornley (1990) states that Hunt (1982) has shown that a young plant grows exponentially.
But Hunt (1982) admits that he had to “force” the linearity between the logarithm of the leaf surface and time. There is also something peculiar about his experiment. The conditions appear not to be constant: The amount of intercepted light increases normally in the period from spring to summer. So, a possible negative deviation from linearity is compensated by an increase in photosynthetic rate.
Other critical remarks are:
First, the experiment doesn’t differentiate between a very young plant depending on the seed for its food supply and an older plant depending entirely on photosynthesis. The growth parameters can be different.
Secondly, a term e-Dt, describing development and differentiation, is questionable as it misses a clearly physiological base.
So, it should not completely be surprising that new analyses of old and new data of oil palm, soybean, sunflower, sage and rice indicate otherwise ( 1, 2, 3, 4): An individual plant shows second order polynomial growth and not exponential growth in the beginning.
Notice, the problem is still actual, see the following paper:
References
Hunt, R., 1982. Plant Growth Curves: The Functional Approach to Plant Growth Analysis. Edward Arnold, London.
Thornley. J.H.M. and I.B. Johnson, 1990. Plant and Crop Modelling: A Mathematical Approach to Plant and Crop Physiology. Clarendon, Oxford.