Introduction
Experiments indicate that plants do not grow exponentially but according a second-order polynomial (link1, link2). An earlier paper (link3) describes how a n-order polynomial is derived from an exponential model. The essence of the reasoning is a shift from the growth machinery to more competitive ability. The question remained why a plant, growing according a second-order will win in a struggle for survival from those not growing according these characteristic.
In an other paper (link4) we saw that a part of a possible explanation is given by a computer simulation showing the second order plants to win form slower (first order) growing plants. In this paper we will evaluate the competition with faster growing (according a third-order polynomial) plants.
Methods
For the methods see link4.
Only the first order plants are replaced by third order plants (see table 1)
Tabel 1: Productive mass (yP(t)), non productive, competitive mass (yNP(t)) and total mass (y(t)) as function of time of plants growing according a polynomial of the second order and the third order. The colour dark red and dark purple indicates the winning order polynomial at that moment: The competitive mass is bigger, i.e. the stem is higher. Dark red is for the plants investing initially more in competitive ability and purple for the plants investing initially more in production. The color green indicates a draw.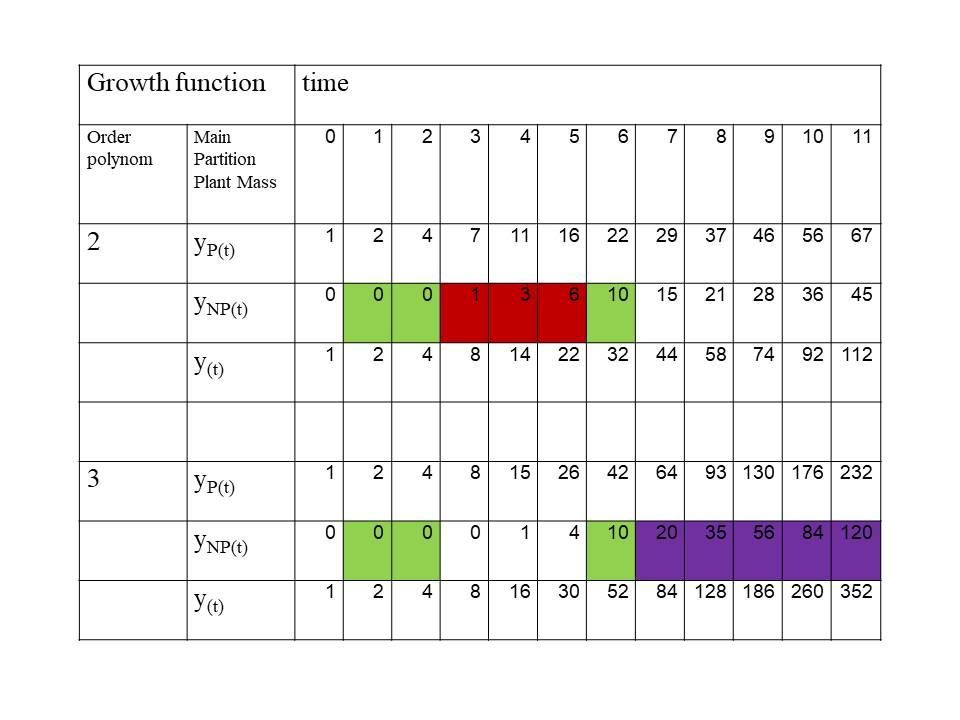
Results and Discussion
(22-8-2020: Notice, the results were corrected as a mistake in the programming caused that only the right side of the plant was competing. It was corrected without making a separate publication, because the main conclusions stayed the same. Moreover, it emphasizes the robustness of the conclusions. Only some numbers changed. )
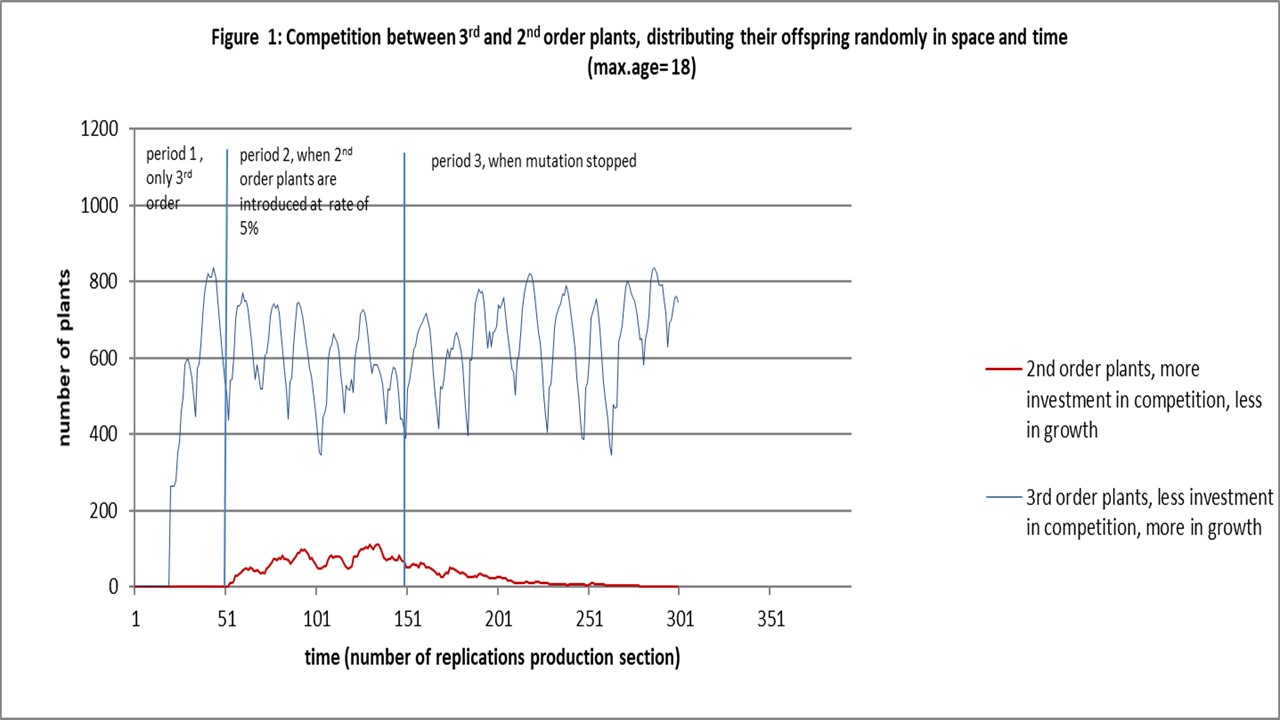
Plants growing according a polynomial of the second order win not from faster growing plants when the distribution of their offspring is randomly in space and time, see figure 1. It does not support the idea of growth according a second order polynomial.
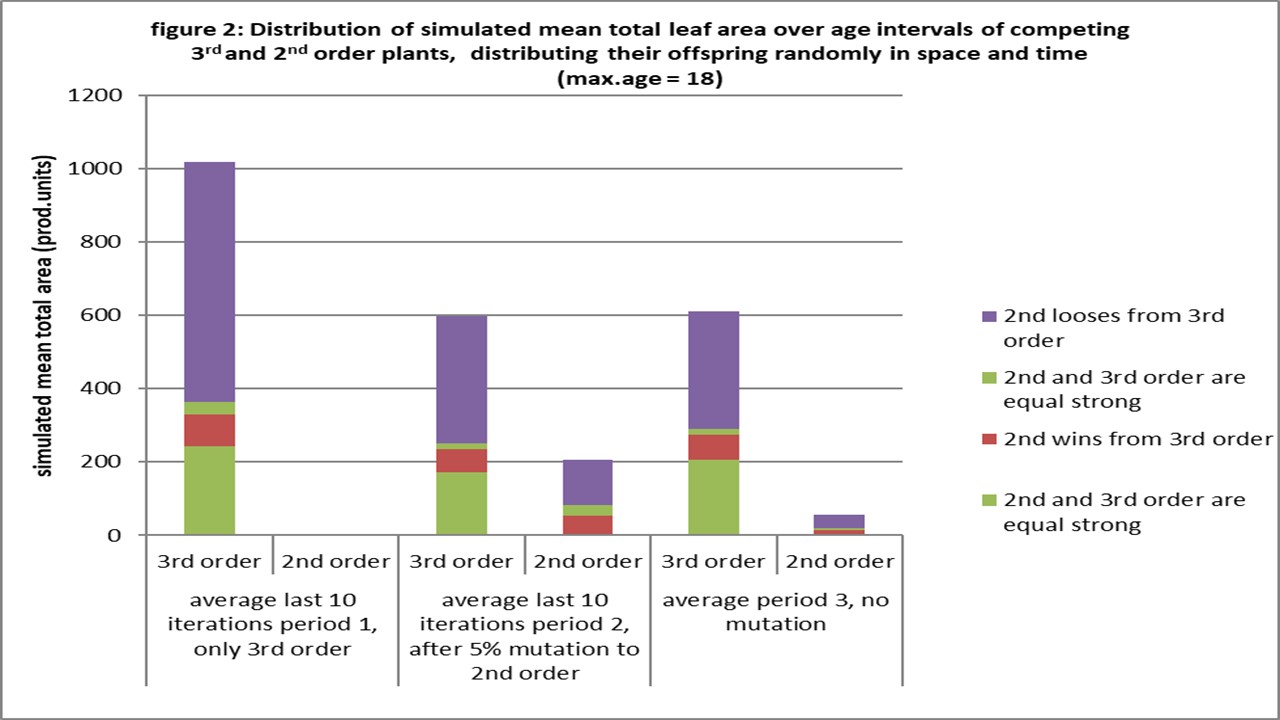
The explanation is simple: Figure 2 shows that the third order plants have more leaf area in the ages when they win from second order. They can suppress a substantial amount of the second order plants when these are introduced.
But when plants concentrate their offspring in time and space it is the opposite.
Now the second order plants win, see figure 3.
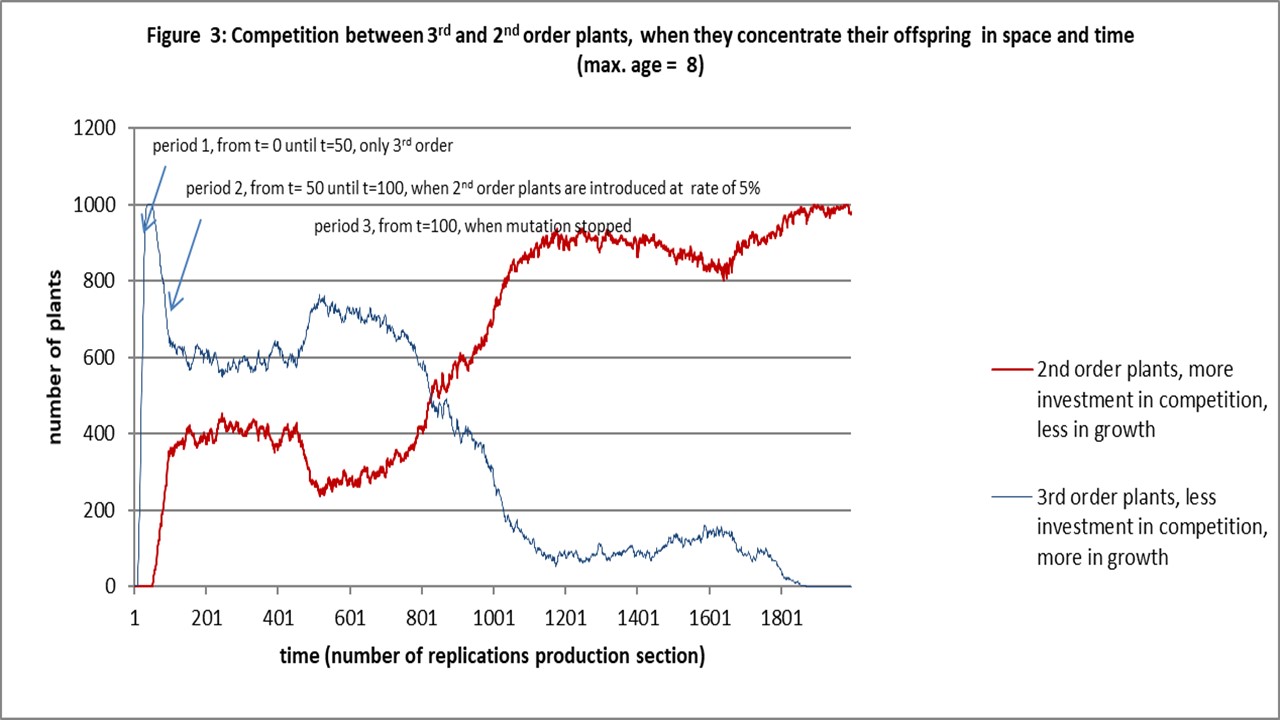
Figure 4 explains it partly, because it is a complicated mechanism. It is clear that due to the high density it is difficult for the plants to escape to the higher ages. There will be a lot meetings of between plants aged 1 or 2 and therefore a lot of draws, see table 1: The assumption ( see methods) was that plants with the same amount of competitive tissue will die then instantly together, when they touch each other. For plants of the 3rd order it is even worse: They have still no competitive issue at age 3 and these plants will show also draws with each other and lower aged plants. The second order plants get here a slight advantage, because they have competitive tissue at age 3, and these investment pays of: They make some space even if it is in their own population. Some plants can escape to the higher ages, clear more area and reproduce at a higher rate. Figure 5 shows this better, when we let the plants at the lower ages out.
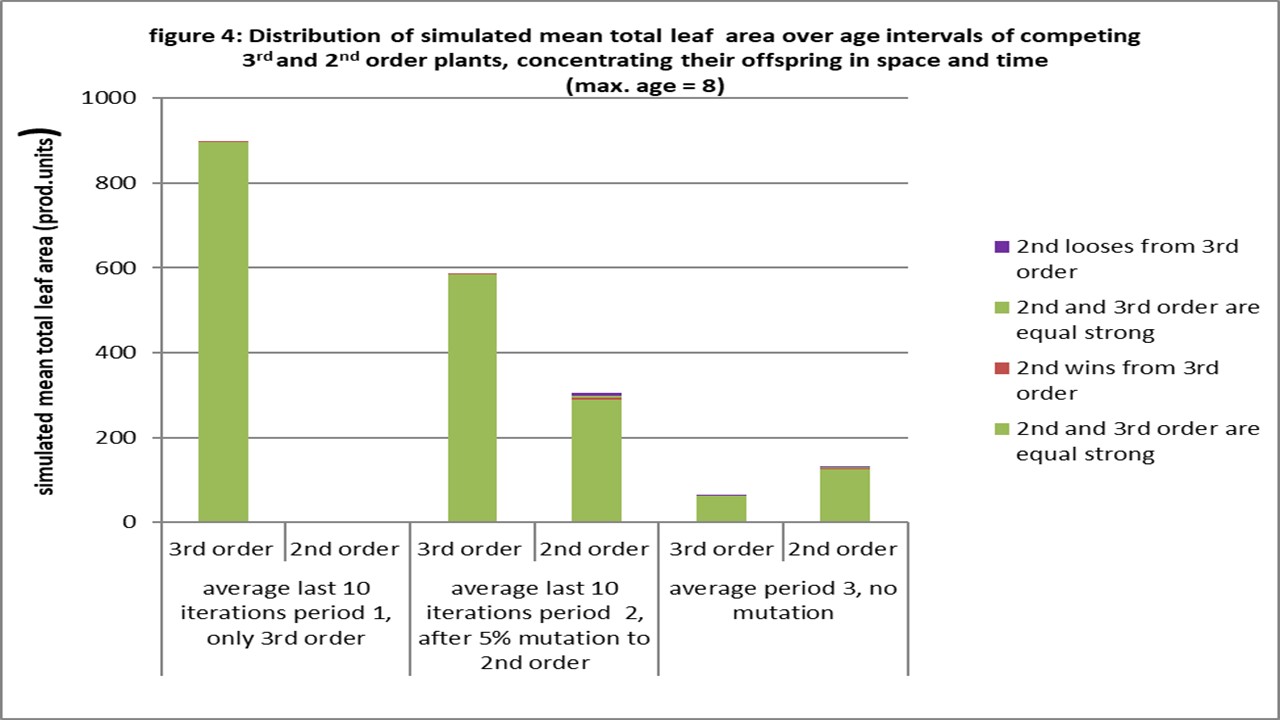
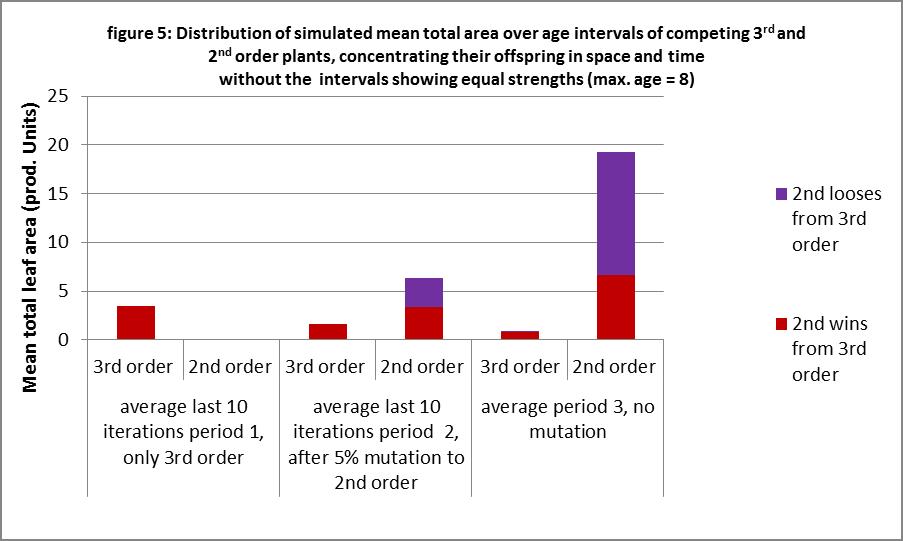
The next question is which situation will occur more: Plants who concentrate their offspring in time and space, giving an advantage for 2nd order plants or plants who do not, giving an advantage to 3rd order plants. Another paper (link5) shows that plants concentrating their offspring win from who don’t.
So, without being a formal proof, the simulation supports the idea that plants will grow rather according a second order than according a third order.
