Introduction
Experiments indicate that plants do not grow exponentially but according a second-order polynomial (link1, link2). An earlier paper (link3) describes how a n-order polynomial is derived from an exponential model. The essence of the reasoning is a shift from the growth machinery to more competitive ability. The question remained why a plant, growing according a second-order will win in a struggle for survival from those not growing according these characteristic.
To find an answer a computer simulation was made where plants growing according a second-order were competing with slower growing (according a first-order polynomial) plant, see paper (link4) and with faster growing  (according a third-order polynomial) plants, see paper (link5). But, it turned out to be important to evaluate a variable, which is unavoidable in the experiment: Is a plant concentrating its offspring around the mother plant or will it generate a random distribution?
(according a third-order polynomial) plants, see paper (link5). But, it turned out to be important to evaluate a variable, which is unavoidable in the experiment: Is a plant concentrating its offspring around the mother plant or will it generate a random distribution?
Methods
See the earlier paper (link4). We built two switches extra to test the question:
- Offspring could change for a certain percentage (0.05) from a distribution in space at random to a distribution more concentrated around the mother plant.
- Offspring could change for a certain percentage (0.05) from a distribution in dormancy at random over a period from 0 to the maximum age to a distribution more concentrated around dormancy 0.
Special attention has to be given to assumption 12, where is stated that the incoming seed will replace the seed already there, if the dormancy is shorter, because it gives implicitly plants concentrating their offspring in time an advantage.
Two simulations were conducted:
- The first experiment started with only one plant. The growth characteristic was a first-order polynomial with random distribution of the seeds over the space of the torus and over the dormancy period from 0 to maximum age (10). It was allowed to grow and multiply to a high density. It means maximal competition. After a certain period we introduced with two mutant switches plants concentrating their offspring in time and space. The switch was set off, when the amount of the mutants reached a percentage of approximately 30. So, the concentrating plants have at that moment still a disadvantage in numbers.
- The second simulation was the same as the first one, only the first order polynomial was replaced by a third order polynomial.
Results and Discussion
20-9-2020: Notice, the results were corrected as a mistake in the programming caused that only the right side of the plant was competing. It was corrected without making a separate publication, because the main conclusions stayed the same, although we had to change the reasoning. It emphasizes to be careful with explanations. Moreover, it introduces a new variable, as plants with a leaf on one side give different results than plants with two leaves, one on each side.
The results of the simulations indicate that first order plants concentrating their offspring in time, i.e. around a dormancy of 0, will win from those who don’t. We already mentioned, while presenting the methods (link4) that we should expect this as assumption 12, i.e. a shorter dormancy wins from a longer one, implicates it.
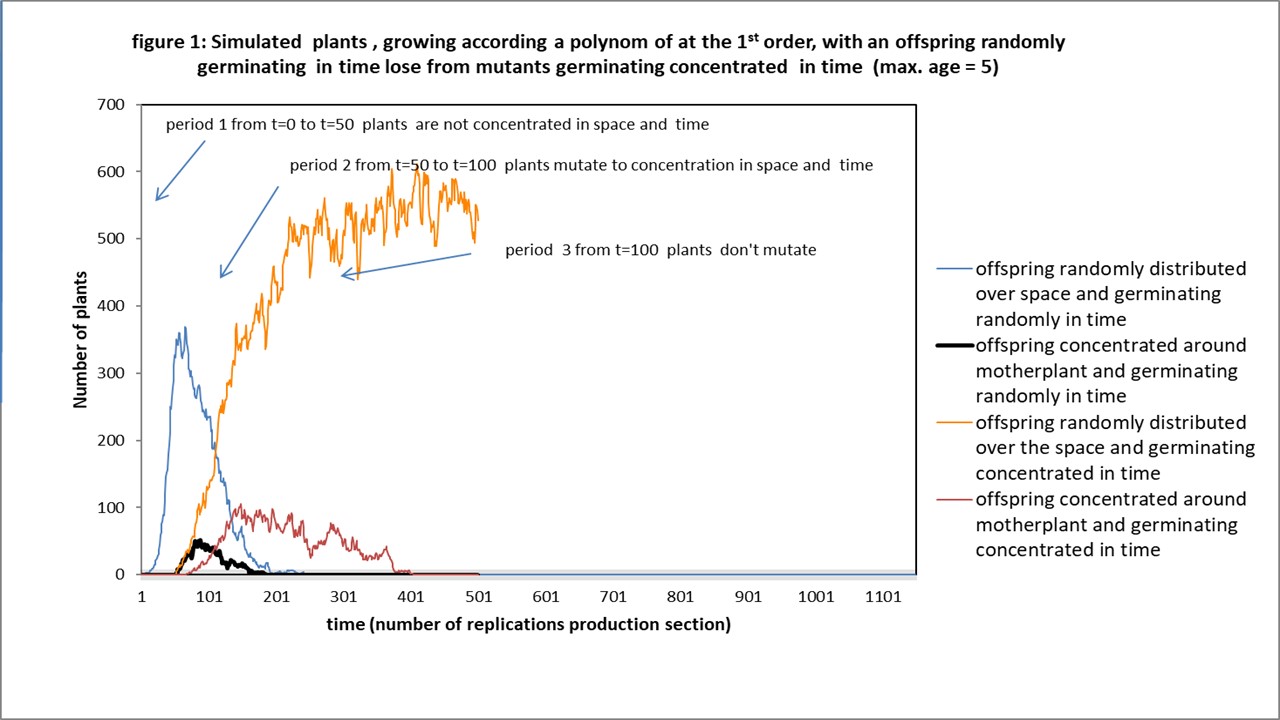
Concentration in space didn’t win. Somehow the intra competition between the concentrating plants is a disadvantage, it is killing too much plants of their own kind. In contrast, in the second experiment, see figure 2, with the third order plants, concentration in space is a winning feature. Here, it prevents invasion form not concentrating plants, while they can invade themselves the population of the not concentrating. The intra competition seems less important.
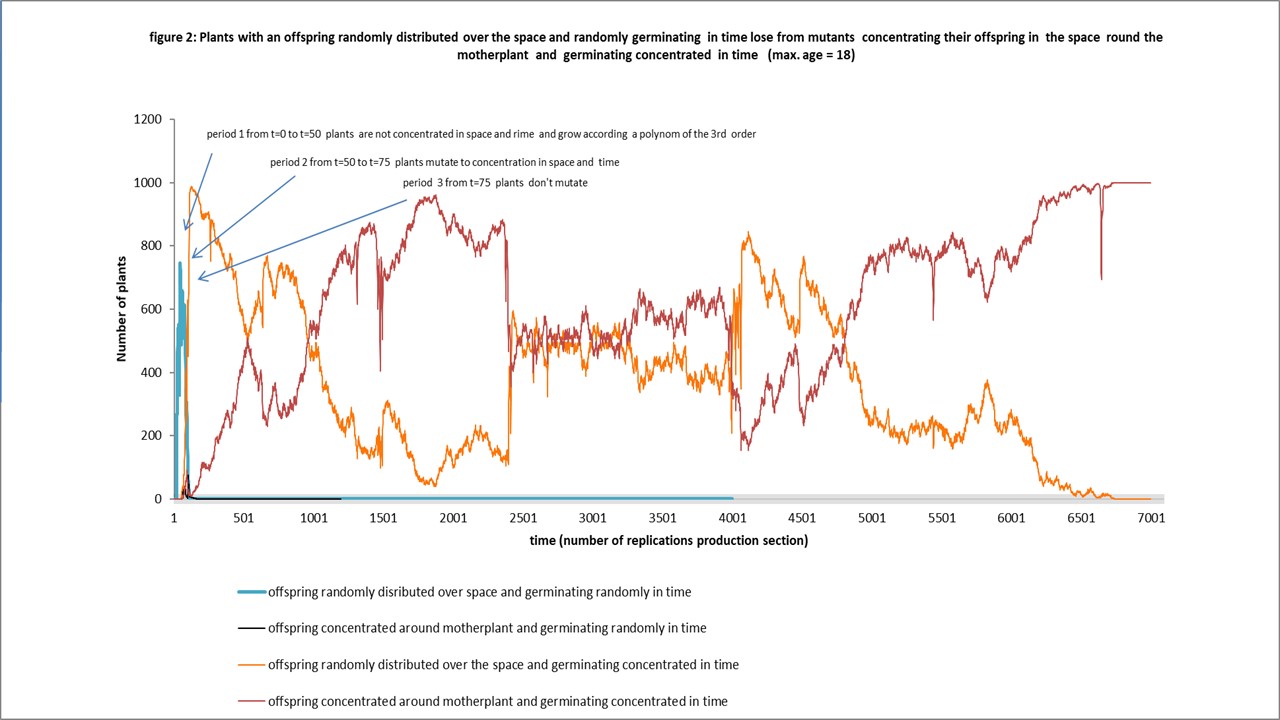
Notice that there will be a shift to another optimal maximum age, for the first order plant it will be 5, for the third order plants 8, see the paper discussing optimal maximum age (link6).
Simulations with second order plants, not mentioned here, showed also concentration in space to be a winning strategy.
The big conclusion is that the first order plants and third order plants will make inevitably a mistake. They will concentrate their populations in time (first order) or time and place (third order) and make a shift in optimal maximum age, i.e. death. But then they will lose from second order as is shown in two other papers (link4), (link5)), while winning when not concentrating.
3-10-2020: The next text had to be added because of the mentioned mistake (only one side of the pant was competing) in programming: With two leaves competing the conclusion was not stable any more for the competition of second order plants and third order plants. The second order plants are making also “inevitably” a mistake. Figure 3 is summarizing what will happen then.
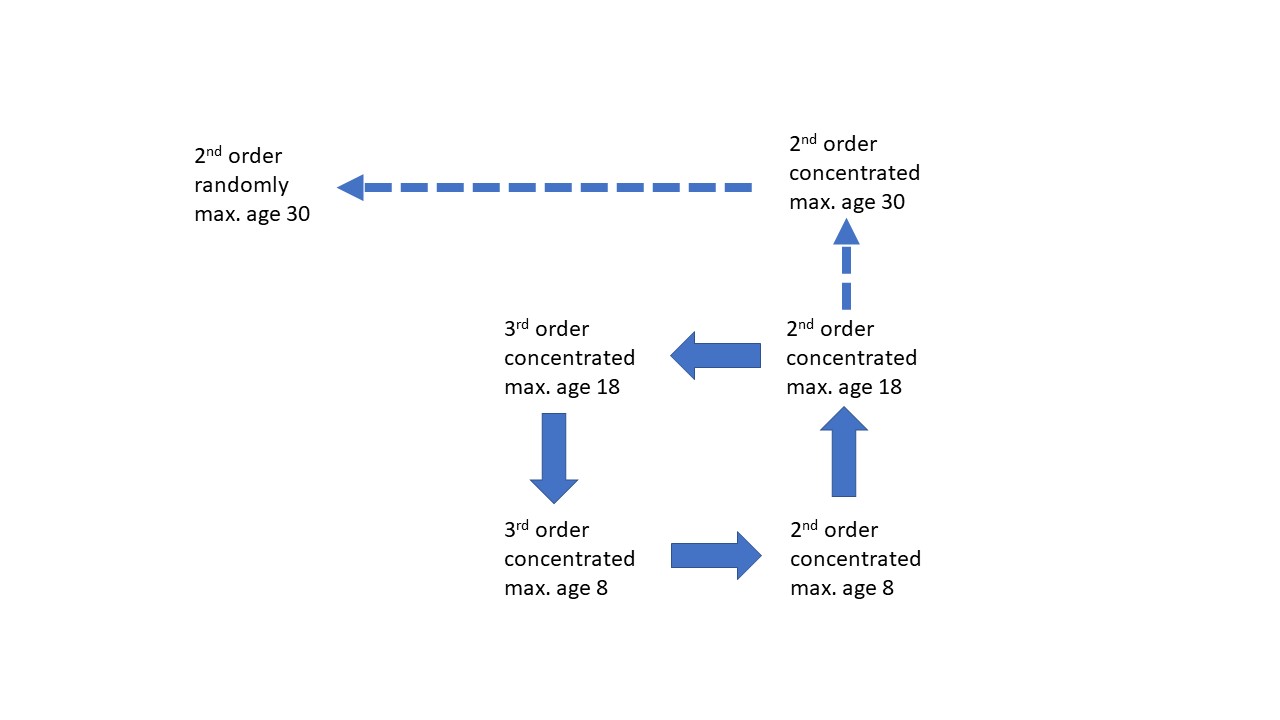
They, aged 8 and concentrating their offspring in space and time, will try to change to their optimal maximum age, i.e 30. If they would reach that age, suddenly third order plants, spreading their offspring randomly in space and time, will win, see the dashed lined arrows. But they will not get there, because they will change already at maximum age 18 to third order plants, now still concentrating their offspring. We get a cycle in the process of second order plants changing to third order plants and then backwards, see the solid lined arrows. You would expect a mixture of second and third order plants. But an extra experiment showed the second order plants, aged 8 and concentrating, win from third order plants, aged 18 and concentrating, while conquering a new empty space. They even win when you add to the mixture second order plants aged 18 and third order plants aged 8. This means that if the second order plants make the mutations, which we called before inevitable, avoidable, by “remembering” to keep concentrating and keeping the maximum age low, i.e. 8, they will conquer empty space better then others with different figures for order growth or maximum age or concentration. It is interesting that information (“remembering”) could be decisive.
Notice: This weakening of the conclusions was not necessary for plants with only on one side a leaf, as the mistake in programming showed: The second order plants still won at their optimal maximum age form third order plants. This opens an extra interesting area of research. It raises for example the question if simulated plants with one leaf on one side can compete with simulated plants with two leafs, one on each side.